239. Sliding Window Maximum 题解（Solution)Leetcode题解

作者:Eason

题目：
用size为k的window划过数组，每次滑过一个element，求每个window中的最大值，以数组的形势return。
比如输入数组nums = [1,3,-1,-3,5,3,6,7], k = 3.

Window position                Max
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

因此, 应该return是 [3,3,5,5,6,7].

思路：

brute force

数组没有排序，因此需要在每个window中一一比较、找到最大，time complexity是O(k)。加上一共有O(n)个window，整个time complexity是O(nk)。

可以在brute force的基础上如何优化呢？

每个window肯定都要看一遍，因此只能优化在window内找最大值。两个相邻window之间有overlap，如果能存下它们的大小关系，每一次移动window就只需要对头尾两个元素操作，即可查出max value。可以做到这一点的data strucutre是heap(priority queue)，这里找最大值我们用max heap。每次slide window的时候remove上一个window最左的元素、add新进入的元素、找到最大元素。add需要O(log k)时间，但是remove一个元素需要先在heap中找到该元素，因此需要O(k)时间。
这里可以做一个优化：把remove放到找最大元素的过程中；不主动remove，从heap顶remove最大的值的过程中，如果元素的index在当前window之外，再remove。这样可以保证每个元素add / remove各一次。所以最后running time是O(nlog k)

继续优化！

再优化就必须让在window内找最大值的速度降为O(1)。也就是说我们要保持最大值在一个位置上，比如每个window的最后一个数，这样才能在取最大值的时候速度为O(1)。但同时maintain这个性质又不能对window里的数字做太多操作，比如排序、partition、search，否则就会慢于O(1)。因此很有可能只能在移动window的时候对之前window的头或尾做一个O(1)的操作。
现在我们重新审视一下sliding window这个strategy。最常见的需要使用sliding window的题目是求window sum，这个strategy在每次移动window的时候减去滑出window的数，再加上新加入的数字。为什么可以直接加上新加入的数字呢？因为每个数字都需要参与sum。如果只求奇数的sum，那要对新加入的数字做判断，如果是偶数就不应该加入window。因此我们发现：sliding window strategy maintains a loop invariant that every element in the window has the potential to be used (loop invariant是算法导论中提到的一个概念，即循环过程中maintain的性质，或者数学等式／不等式)。对于这个题，我们要保证进入window的元素一定has the potential to be a max！
具体做法是，对欲加入window的元素和window中的元素做比较，欲加入的元素大，则删掉window中的元素。因为window往前移动的过程中，一个较小的数如果排在一个较大的数后面，这个数肯定不能成为max。这样可以保持max在sliding window最左边。
但是立刻这个思路又遇到一个问题：从window最右端开始，要往左看几个元素？如果往左看multiple elements都比欲加入元素小，那这些排在后面的较小的元素都不可能成为最大，那是不是又要套一个循环、running time不能是O(1)了呢？其实不然，因为做比较这个loop在每一个window执行的次数有多有少，说到底每个元素还是只被add和remove了一次，搜索到每个元素然后remove也只需要往前找一个，即O(1)的时间。

题解：

heap方法


class Solution {
    // use Elem class to wrap value and its index
    // in order to compare idx when pop out
    class Elem {
        int val;
        int idx;
        
        Elem(int val, int idx) {
            this.val = val;
            this.idx = idx;
        }
        
        public int getVal() {
            return val;
        }
        
        public int getIdx() {
            return idx;
        }
    }
    
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || k <= 0) {
            return new int[0];
        }
        
        int[] maxs = new int[nums.length - k + 1];
        // max heap
        Queue queue = new PriorityQueue<> ((e1, e2) -> e2.val - e1.val);

        for(int i = 0; i < k; i ++){
            queue.add(new Elem(nums[i], i));
        }
        maxs[0] = queue.peek().getVal();
        for(int i = k; i < nums.length; i++){
            queue.add(new Elem(nums[i], i));
            while(queue.peek().getIdx() <= i-k) {
                queue.remove();
            }
            maxs[i - k + 1] = queue.peek().getVal();
        }

        return maxs;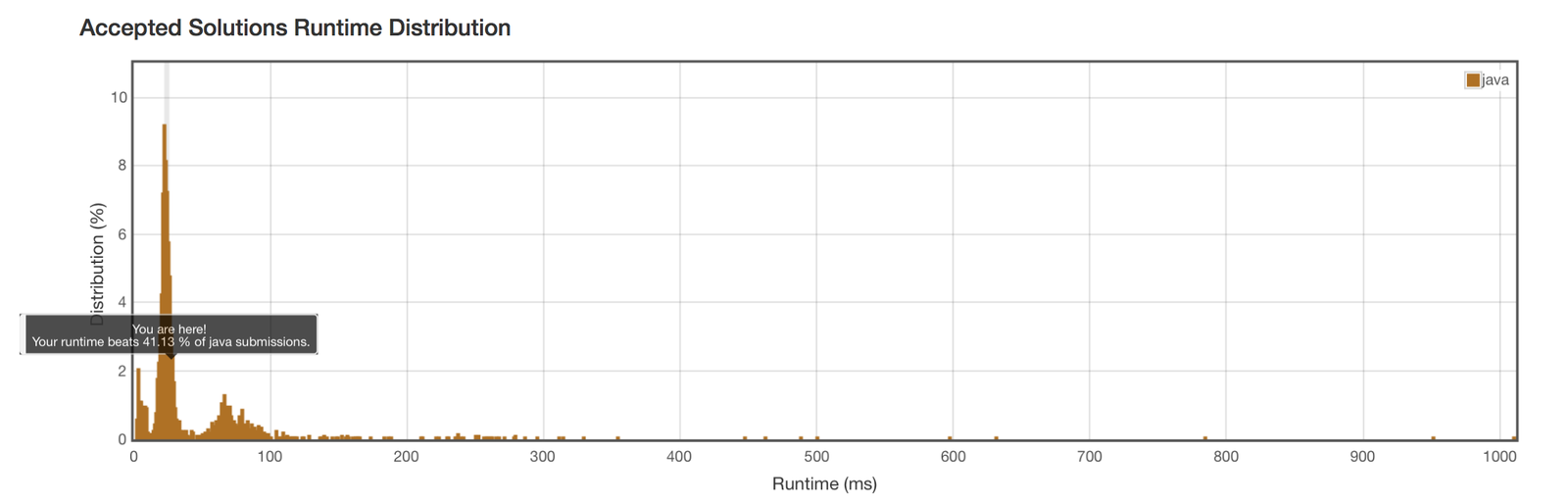
    }
}

deque方法


class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || k <= 0) {
            return new int[0];
        }
        
        int[] maxs = new int[nums.length - k + 1];
        Deque window = new LinkedList<> ();
        for (int i = 0; i < nums.length; i++) {
            // compare and select numbers potential to be max
            while (!window.isEmpty() && nums[window.peekLast()] <= nums[i]) {
                window.removeLast();
            }
            // remove number slided out of window, here is why store index in window
            if (!window.isEmpty() && window.peekFirst() < i + 1 - k) {
                window.removeFirst();
            }
            window.addLast(i);

            if (i + 1 - k >= 0) {
                maxs[i+1-k] = nums[window.peekFirst()];
            }
        }
        return maxs;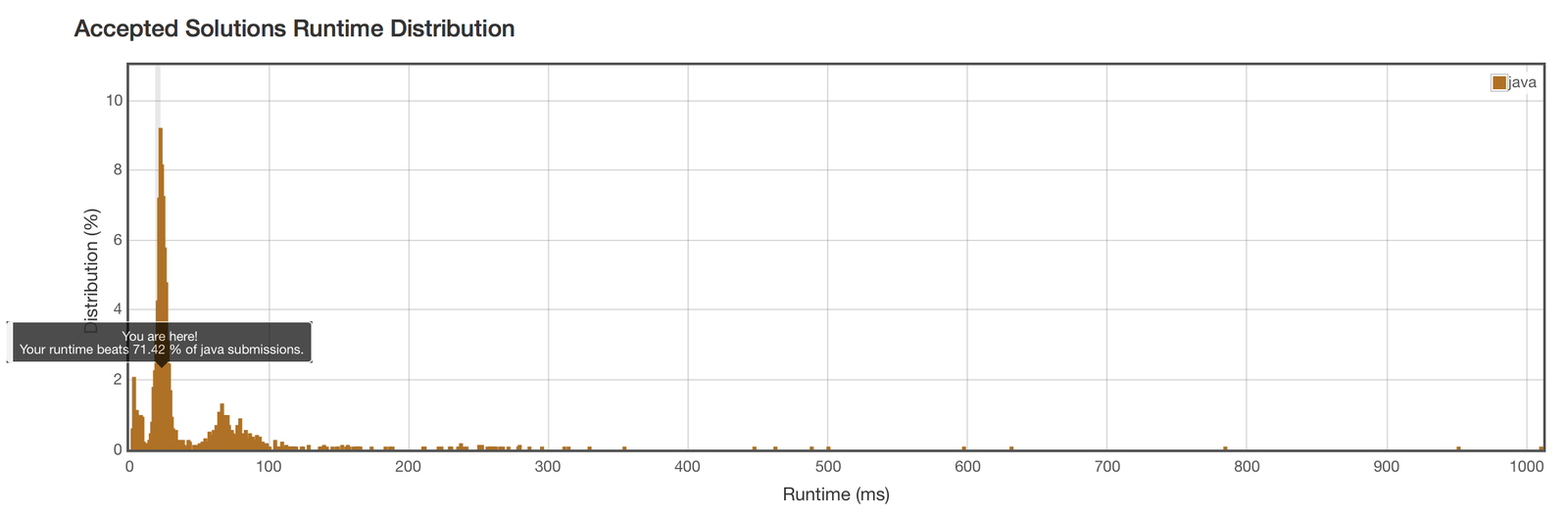
    }
}

follow-up:

这篇帖子针对deque的解法，给出了一种generic的写法、可能可以用在工作实践当中。

https://leetcode.com/problems/sliding-window-maximum/discuss/65885

同这里deque方法的time complexity分析一样的题目有很多，比如longest substring with at most k distinct characters这一题，sliding window的做法也是O(n).


public class Solution {
    public int lengthOfLongestSubstringKDistinct(String s, int k) {
        int[] count = new int[256];     // there are 256 ASCII characters in the world

        int i = 0;  // i will be behind j
        int num = 0;
        int res = 0;

        for (int j = 0; j < s.length(); j++) {
            count[s.charAt(j)] += 1;
            if (count[s.charAt(j)] == 1) {    //  distinct character
                num += 1;
            }
            while (num > k && i <= j) {     // sliding window
                count[s.charAt(i)]--;
                if (count[s.charAt(i)] == 0){ 
                    num--;
                }
                i++;
            }
            res = Math.max(res, j - i + 1);
        }
        return res;
    }
}